モンティ・ホール問題という定理をご存知でしょうか。
定理というか確率の問題といってもいいかもしれません。それを上手く歴史小説に織り込んだ作品が光秀の定理です。

モンティ・ホール問題に関しては非常におもしろいので、一度記事にしてみたいとずっと考えていました。誰もが間違う確率の問題といっていいでしょう。私も最初はまったく理解できませんでした。
モンティ・ホール問題とは何か?
モンティ・ホール問題とは正解の扉を選ぶクイズ番組です。
三つの扉があり、このうち一つの扉の向こうには豪華賞品が置かれています。挑戦者はその扉を当てると豪華賞品を手にすることができます。クイズ番組の司会者は最初からどの扉が正解なのかを知っています。
三つの中から挑戦者が一つの扉を選びました。
クイズ番組の司会者は残された扉のうちの一つを開き、空であることを示しました。そして挑戦者に再度選択権を与えました。
扉を選び直しますか?それとも最初に選んだ扉をそのまま選択しますか?
モンティ・ホール問題の解説
状況を整理します。
- 三つの扉があり、そのうち一つが当たり
- 挑戦者は扉を一つ選ぶ
- 司会者が残った扉のうち一つを開き、空であることを示す
- 残りの扉のうちどちらかが当たり
- 扉を選び直すべきかどうか?
最初にある扉は三つ

この時点で挑戦者が選んだ扉が当たりである可能性は三分の一ですね。ここまでは何も問題ありません。
挑戦者が扉を一つ選ぶ
挑戦者が一番左側の扉を選んだとします。

挑戦者が選んだ扉が正解である可能性は三分の一です。ここも特に問題はないですね。
答えを知っている司会者がヒントをくれる
答えを知っている司会者が一番右側の扉を開いて、ハズレの扉であることを教えてくれました。

残された扉は二つです。この中のどちらかが当たりの扉です。
扉が二つ残されていて、どちらかが当たりなので、確率は二分の一、ではないのです。
スポンサーリンク
扉を変えた方が当たる確率は高くなる
扉が三枚のケース
残された扉が二つあり、どちらかが当たりなのだから50%の確率だろう、と誰もが思います。私も最初はそう考えました。解説を聞いても、しばらくの間は理解できませんでした。
直感で間違ってしまう理由は、最初の前提を忘れてしまうからです。

3枚の扉があるときに、1枚の扉が当たりである確率は三分の一です。残りの2枚は三分の二の確率で当たります。

そして当たりを知っている司会者が、残りの2枚のうちの1枚を開いてくれました。
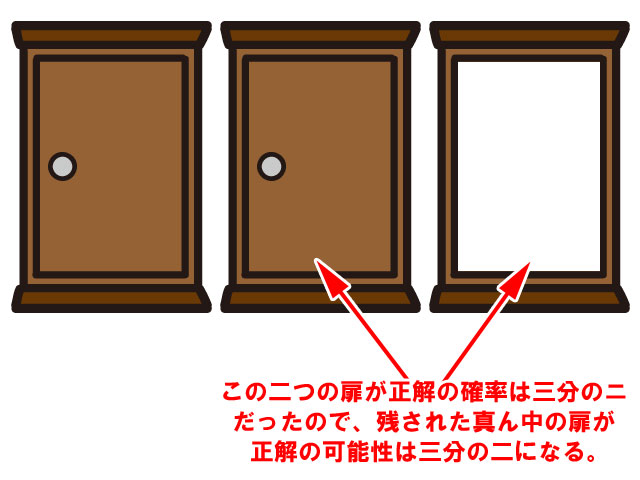
残された扉の2枚が当たりである可能性は三分の二でした。
そのうち一枚の扉がハズレであることを司会者が教えてくれたので、真ん中の扉が正解である可能性は三分の二です。
つまり選び直した方が正解する確率は高くなるのです。
扉が十枚のケース
扉の枚数を増やすともっと分かりやすくなります。一気に十枚まで増やしてみましょう。

十枚の扉があって、そのうちの一枚を選択した場合、その扉が当たりである確率は10分の1ですね。
では残りの扉の中に当たりが含まれている確率はいくらでしょうか。

分かりやすいようにグループ分けしてみました。
選択した扉が当たりである可能性は10分の1であることは変わりません。そして残された扉の中に正解がある可能性も10分の9のままです。

ハズレの扉を開いてみても、元々の確率は変わりません。
つまり枚数が多くなればなるほど、変更した時に当たりの扉を引く可能性は高くなるのです。
光秀の定理でのモンティ・ホール問題の使われ方
光秀の定理には、兵法者の新九郎と破戒僧の愚息という人物が登場します。小説のオリジナルキャラクターですね。
劇中でモンティ・ホール問題を利用して、博打を行って小銭を稼いでいたのが愚息という僧侶です。辻博打なので、扉ではなく4つのお椀を使用して博打を行っていました。
この二人がふとしたことから光秀と親しくなり、やがて光秀は城の攻略戦で愚息の知恵を借りるのです。
まとめ ー 誰もが直感だと間違えるおもしろい確率の問題
書評よりもモンティ・ホール問題の解説の方が多くなってしまいましたが、それだけおもしろい確率の問題でもあります。
それを歴史小説に上手く織り込んだのが「光秀の定理」という作品です。前述したように、愚息がこの問題を使って博打で小銭を稼いでいるのですが、それが光秀の長光寺城の攻略に繋がるあたりは、ここでこの問題を持ってきたか!、とちょっとしびれる感じがあります。
こういう新しい切り口の歴史小説は楽しいですね。



